1
2
3
4
5
6
7
8
9
10
11
12
#Load in packages
from siphon.catalog import TDSCatalog, Dataset
import pandas as pd
import numpy as np
import metpy
import cartopy.crs as ccrs
import holoviews as hv
from holoviews import opts
import xarray as xr
import hvplot.xarray 
from geoviews import tile_sources as gvts
import panel as pn

1
2
hv.extension('bokeh')
hv.output(size=250)

1
2
3
#Get the list of current files on the THREDDS server
#Note that the TDSCatalog takes the url of the folder you want the files from as an argument
cat = TDSCatalog('https://thredds.ucar.edu/thredds/catalog/grib/NCEP/RTMA/CONUS_2p5km/latest.xml')

1
2
#Now let's look at the dataset that are available
cat.datasets

1
2
3
nc2 = cat.datasets[0].access_urls
nc3 = xr.open_dataset(nc2['OPENDAP']).metpy.parse_cf() # Parse with metpy to make it easier to plot
nc3 = nc3.metpy.assign_latitude_longitude() # Latitude and Longitude are not included, so have metpy add them

1
list(nc3.keys())

1
nc3['Temperature_Analysis_height_above_ground']

1
2
3
4
5
6
inds = []
[inds.append(x) for x in nc3.variables if 'Temperature' in x or 'temperature' in x]
for ind in inds:
    nc3[ind] = nc3[ind]-273.15
    nc3[ind].attrs['units'] = 'C'
nc3['Temperature_Analysis_height_above_ground']

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def plot(var=None):
    # Choose the basemap from geoviews tile_source
    base_map = gvts.StamenTerrain
    
    # Create a hvplot quadmesh, call is similar to xarray.plot()
    # For each variable, we want all the values for each dimension, except for 
    #      height_above_ground since it can only take on one value
    # We want to plot the variable on a lat/lon grid, so we set x and y to lon/lat.
    # Rasterize = True helps to speed up the plotting/display
    #
    # For our example, we are only using one time step. If we had more than one time step, 
    #      the groupby call would make a holoviews widget next to the graph that would
    #      allow for the time to be changed and the plot would then update.
    mesh = nc3[var][:,0,:,:].hvplot.quadmesh(x='longitude', y='latitude',
                                rasterize=True, geo=True, title=' '.join(var.split('_')[0:2]),
                                crs=ccrs.PlateCarree(),
                                groupby=list(nc3[var].dims[0:1]), 
                                cmap='jet').opts(frame_width=200, 
                                frame_height=200, colorbar=True, axiswise=True)
    
    # Now we want to overlay the hvplot.quadmesh onto the basemap and include the wheel_zoom tool
    #     from Bokeh to allow the user to zoom in and out on the map. NOTE: There are many other
    #     Bokeh tools that can be used, see the Bokeh documentation for more info:
    #     https://docs.bokeh.org/en/latest/docs/user_guide/tools.html
    overlay = (base_map * mesh.opts(alpha=0.7)).opts(active_tools=['wheel_zoom'])
    
    # Return the holoviews plot
    return overlay

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Widget to select the variable. We start with a panel Select widget
# We provide the name for it to display above it (name), the options within it,
#     and the starting value when it loads. NOTE: We are taking variables after
#     the first 2 in the list since the first two describe the projection and 
#     time boundaries.
var_select = pn.widgets.Select(name='Variables:', options=list(nc3.keys())[2:], 
                               value='Temperature_Analysis_height_above_ground')

# Define a function to call the plotting function when a new variable is chosen
def on_var_select(event):
    var = event.obj.value
    dashboard[-1] = plot(var=var)

# Function to watch the var_select widget event and call the on_var_select function 
#     when it is updated.
var_select.param.watch(on_var_select, parameter_names=['value']);

1
2
3
4
5
6
7
# Create the dashboard. We want them to be organized in a column, with the variable select
#     menu on the top and the plot below it

# Please note that using this in browser, changing variables may not work. Download this notebook and run it on your own
#     to experience the full effects!
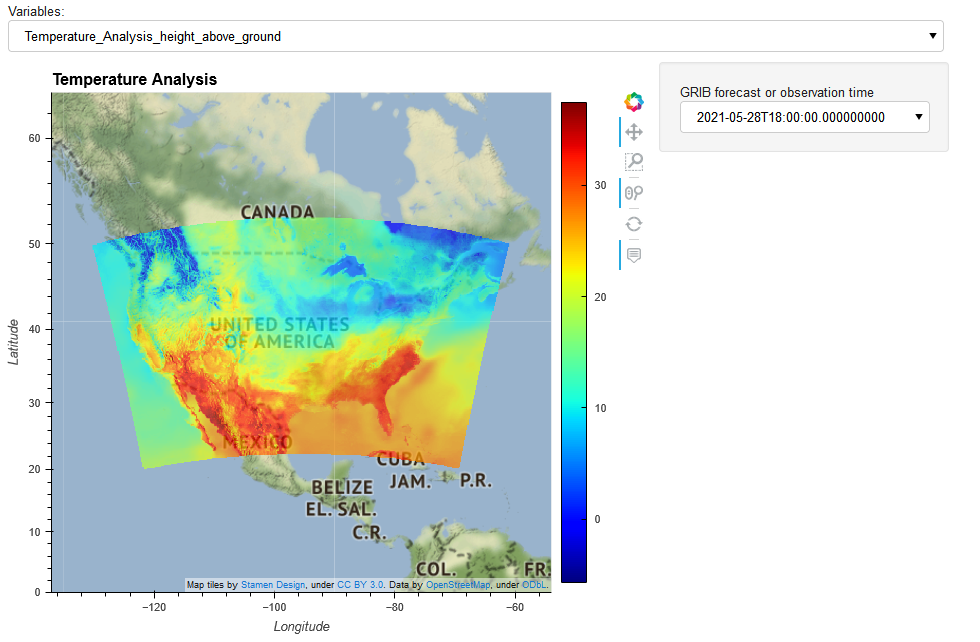
dashboard = pn.Column(var_select, plot(var_select.value))
dashboard

1